Binomial theorem(이항계수)
- 이항계수(binomial theorem) 알고리즘 : 조합론에서 사용되며, n개의 서로 다른 원소에서 r개의 원소를 선택하는 경우의 수를 계산
- 이항계수 : 조합론에서 등장하는 개념으로 주어진 크기 집합에서 원하는 개수만큼 순서없이 뽑는 조합의 가짓수 / 2를 상징하는 ‘이항’이라는 말이 붙은 이유는 하나의 아이템에 대해서는 ‘뽑거나, 안 뽑거나’ 두 가지의 선택만 존재
(ex)4개의 집합 중에서 2개를 순서없이 고르는 조합의 수는 ‘4! / 2! / 2!’, 즉 6
nCk = n! / k!(n-1)! = (4*3*2*1) / (2*1)(2*1) = 3*2*1 = 6
1. r이 0이거나 n과 같으면 함수는 1을 반환
2. 그렇지 않으면 k-1과 n-1인자로하여 자기 자신을 두 번 호출하고 두 결과의 합을 반환
3. 이 과정은 k가 0이나 n과 같아질 때까지 반복
Java예시

- k가 0이나 n과 같아지면, 값을 return함
- k-1과 n-1, n-1과 k인자로하여 자기 자신을 두 번 호출하고 두 결과의 합을 반환
- main함수에서 실행한 결과
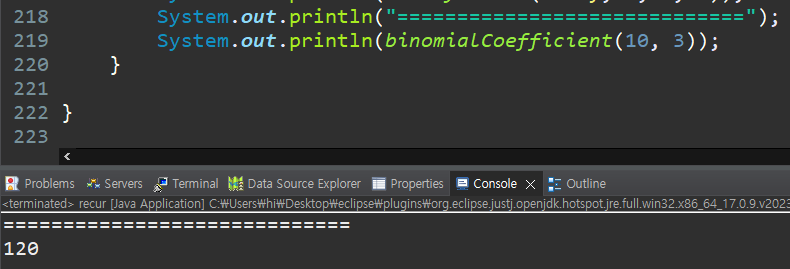
nCk = n! / k!(n-1)! = (10*9*8*7*6*5*4*3*2*1) / (3*2*1)(7*6*5*4*3*2*1) = (10*9*8)/(3*2*1) = 720/6 = 120
C예시 - 추가 예정
'Data Structure > Algorithm' 카테고리의 다른 글
| Recursive Algorithm - GCD(최대공약수) (0) | 2024.04.09 |
|---|---|
| Recursive Algorithm - Fibonacci (0) | 2024.04.08 |
| Recursive Algorithm - Recursive Function (1) | 2024.04.07 |
| Sort Algorithm - Heap (0) | 2024.04.01 |
| Sort Algorithm - Quick (0) | 2024.03.31 |



