Heap
- Heap = 최솟값과 최대값을 빠르게 찾아내기 위해 완전2진트리 형태로 만들어진 data structure
Heap이 가지는 기본 특성
left child node = index * 2 + 1
right child node = index * 2 + 2
parent node = (index-1) / 2
- 오름차순 정렬 : 최대 Heap, 내림차순 정렬 : 최소 Heap 사용
최대 Heap : Parent node의 value(key value) <= Child node의 value
최소 Heap : Parent node의 value(key value) >= Child node의 value
Java예시

HeapSort() : Heap Sort Algo. 실행
sort1() : heapify()를 이용해 Max Heap을 얻는 함수
if(size<2){return;} : Parent node를 이용해 heapify하는 과정에서 -정수가 발생하면 참조 오류가 발생하므로 element의 개수가 적을 때는 굳이 Heap Sort를 쓸 필요까지 없어 바로 종료시키는 조건
int parentIdx = getParent(size-1); : 가장 마지막 element의 parent index
for(int i = parentIdx; i >=0; i--){heapify(a, i, size-1);} : max Heap 구하기
for(int i = parentIdx; i >=0; i--){ swap(a, 0, i); heapify(a, i, size-1);} : Root의 0번째 index와 i번째 index 서로 교환 후 0~(i-1)까지의 부분 tree에 대해 max heap을 만족하도록 재구성
getParent() : parent의 index를 얻는 함수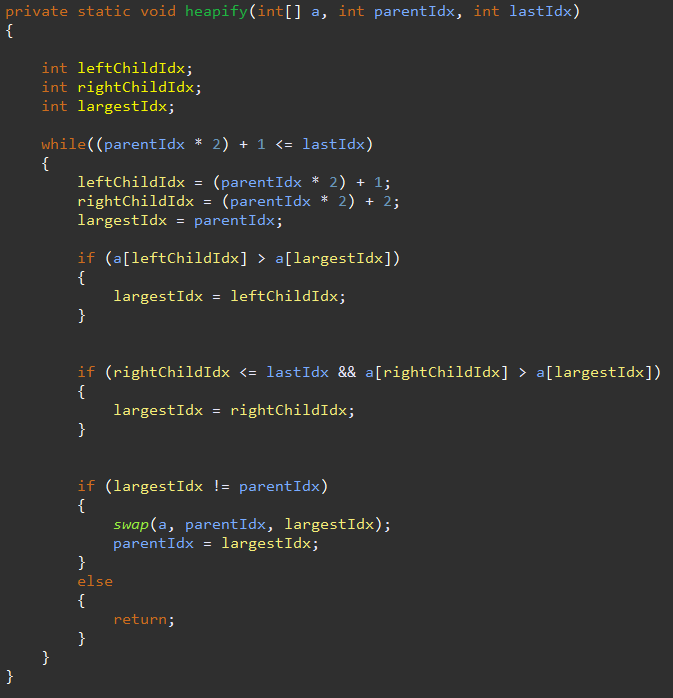
- heapify() : Heap정렬 수행
현재 Parent index의 child node의 index가 마지막 index를 넘지 않을 때까지 반복(왼쪽 child node를 기준으로 진행)if(a[leftChildIdx] > a[largestIdx] ){ largestIdx = leftChildIdx ;} : left child node와 비교
if(a[rightChildIdx] > a[largestIdx] ){ largestIdx = rightChildIdx ;} : right child node와 비교
if( largestIdx != parentIdx ){swap(a, parentIdx, largestIdx); parentIdx = largestIdx;} else{return;} : 교환 발생시 2개 element 교체 후 교환된 child node를 Parent node로 교체
- main함수에서 실행한 결과

C예시
- 추가 예정
'Data Structure > Algorithm' 카테고리의 다른 글
| Recursive Algorithm - Fibonacci (0) | 2024.04.08 |
|---|---|
| Recursive Algorithm - Recursive Function (1) | 2024.04.07 |
| Sort Algorithm - Quick (0) | 2024.03.31 |
| Sort Algorithm - Merge (0) | 2024.03.30 |
| Sort Algorithm - Shell (0) | 2024.03.29 |



